Detaljert analyse av RC Series Circuit
2024-05-08
20571
RC -seriekretsen, bestående av en motstand og en kondensator, fungerer som en grunnleggende komponent i både grunnleggende og avanserte elektroniske systemdesign.Det hjelper til å forstå sentrale prinsipper som frekvensrespons, faseskift og signalfiltrering, som spiller en betydelig rolle i kretsdesign og signalbehandling.Denne utforskningen dekker teoretiske grunnleggende og strekker seg til praktiske anvendelser gjennom eksperimenter og simuleringer.Ved å fysisk montere kretsen eller modellere den digitalt, kan elevene visuelt ta tak i ladeprosessen og effekten av komponent V ariat -ioner, noe som gjør komplekse konsepter mer tilgjengelige og minneverdige.
Katalog

Figur 1: Ulike utgangsspenninger av RC -kretser
Introduksjon til RC Circuit
En RC-krets, forkortelse for resistenskapasitanskrets, er grunnleggende i elektronikk for å manipulere signaler gjennom motstander og kondensatorer.Disse kretsene er spesielt kjent for sin evne til å skifte faser og filtersignaler ved å bruke enkle arrangementer av disse komponentene.En grunnleggende RC-krets, ofte referert til som en førsteordens RC-krets, inkluderer vanligvis bare en motstand og en kondensator.
I et typisk oppsett blir inngangsspenningen påført seriearrangementet av en motstand og en kondensator.Utgangen kan trekkes enten over motstanden eller kondensatoren, og hver gir forskjellige svar på signalfrekvenser på grunn av kondensatorens unike egenskaper.Denne allsidigheten gjør at RC -kretser kan utføre en rekke roller i elektroniske enheter, for eksempel koblings- og filtreringssignaler eller til og med konvertere bølgeformer når den utsettes for en trinnspenning.
RC-kretsen kan konfigureres på flere måter-serier, parallell eller en kombinasjon av begge, kjent som serie-parallell.Hver konfigurasjon påvirker signalfrekvensene annerledes: seriekoblinger har en tendens til å dempe lave frekvenser, mens parallelle tilkoblinger brukes til å dempe høyere frekvenser.Denne forskjellen skyldes først og fremst måten motstander og kondensatorer samhandler med kretsen;Motstander er direkte imot strøm mens kondensatorer lagrer og frigjør den, og påvirker hvordan kretsen reagerer på forskjellige frekvenser.
I motsetning til kretsløp som inkluderer induktorer, som LC -kretser, kan ikke enkle RC -kretser resonere siden motstander ikke lagrer energi.Denne attributtet påvirker tydelig hvordan RC -kretser brukes, med fokus på deres kapasitet for filtrering snarere enn energilagring eller resonans.Hver konfigurasjon tjener et spesifikt formål, noe som gjør RC -kretser allsidige verktøy i både teoretisk studie og praktisk anvendelse i elektronisk design.
RC Series Circuit
En RC -seriekrets, i hovedsak sammensatt av en motstand (R) og en kondensator (C) i serie, opererer etter et greit prinsipp.Når kretsens bryter er lukket, begynner kondensatoren å lade fra den påførte spenningen (V), initierer en strøm av strøm gjennom kretsen.Når kondensatoren lades, øker strømmen gradvis til kondensatoren når sin kapasitet, på hvilket tidspunkt den slutter å akseptere ladningen, og strømmen stabiliseres med sin maksimale verdi, beregnet som 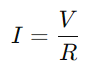 .
.
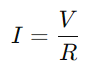 .
.Ladingsprosessen til kondensatoren kan beskrives matematisk av ligningen 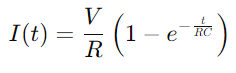 , hvor jeg er strømmen, V er spenningen, R er motstanden, C er kapasitansen, t er tid, og e er basen til den naturlige logaritmen.Denne formelen gjenspeiler hvordan strømmen endres over tid som kondensatoren lades, med produktet av motstands- og kapasitansverdiene (RC) som definerer tidskonstanten til kretsen, noe som indikerer hastigheten som kondensatoren lades.
, hvor jeg er strømmen, V er spenningen, R er motstanden, C er kapasitansen, t er tid, og e er basen til den naturlige logaritmen.Denne formelen gjenspeiler hvordan strømmen endres over tid som kondensatoren lades, med produktet av motstands- og kapasitansverdiene (RC) som definerer tidskonstanten til kretsen, noe som indikerer hastigheten som kondensatoren lades.
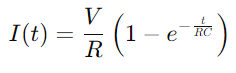 , hvor jeg er strømmen, V er spenningen, R er motstanden, C er kapasitansen, t er tid, og e er basen til den naturlige logaritmen.Denne formelen gjenspeiler hvordan strømmen endres over tid som kondensatoren lades, med produktet av motstands- og kapasitansverdiene (RC) som definerer tidskonstanten til kretsen, noe som indikerer hastigheten som kondensatoren lades.
, hvor jeg er strømmen, V er spenningen, R er motstanden, C er kapasitansen, t er tid, og e er basen til den naturlige logaritmen.Denne formelen gjenspeiler hvordan strømmen endres over tid som kondensatoren lades, med produktet av motstands- og kapasitansverdiene (RC) som definerer tidskonstanten til kretsen, noe som indikerer hastigheten som kondensatoren lades.
Figur 2: RC Series Circuit
Utladning oppstår når bryteren åpnes, og reverserer prosessen: den lagrede energien i kondensatoren frigjøres, noe som får strømmen til å strømme i motsatt retning til kondensatoren er tappet.Denne lade- og utladningssyklusen er avgjørende i applikasjoner som signalkonvertering, filtrering og timingskretser på grunn av den forutsigbare måten strømmen og spenningsendringen.

Figur 3: RC Series kortslutning
Oppførselen til RC -seriekretsen varierer også med frekvens.Ved lave frekvenser fungerer kondensatoren mer som en åpen krets, og hindrer strømmen av strøm.Når frekvensen øker, avtar den kapasitive reaktansen, noe som gjør det lettere for strømmen å passere gjennom.Denne endringen i impedans med frekvens gjør det mulig for RC -seriekretsen å fungere som et filter, og selektivt dempe frekvensene under en vis 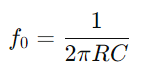 ).
).
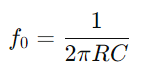 ).
).
Figur 4: Lading og utskrivning av RC -seriekretser
I tillegg til stabil tilstand, blir RC-kretser også studert for sine forbigående svar når de blir utsatt for plutselige endringer i spenning, for eksempel når en DC-strømforsyning er slått på eller av.Dette scenariet kalles en forbigående prosess, der kretsen overgår fra en stabil tilstand til en annen.Dynamikken i denne prosessen avhenger betydelig av RC -tidskonstanten, som styrer hvor raskt kretsen reagerer på endringer.
Til syvende og sist tjener RC -seriekretser flere funksjoner i både DC- og AC -applikasjoner, og håndterer oppgaver som spenner fra å forsinke signaler til integrering eller kobling av forskjellige kretselementer.Denne allsidigheten stammer fra de unike interaksjonene mellom motstanden og kondensatoren, som til sammen bestemmer den totale responsen til kretsen på endringer i spenning og frekvens.

Figur 5: RC Series kretsdiagram og frekvensformel
I en RC -seriekrets, samspillet mellom motstanden (R) og kondensatoren (C) påvirker både strømstrøm og spenningsfordeling.Motstandens primære rolle er å regulere den nåværende strømmen.Dette forholdet blir kvantifisert etter Ohms lov, som sier 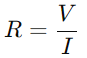 , hvor V er spenning og jeg er aktuell.I hovedsak fungerer motstanden som en flaskehals, og kontrollerer hvor mye strøm som kan passere gjennom til enhver tid.
, hvor V er spenning og jeg er aktuell.I hovedsak fungerer motstanden som en flaskehals, og kontrollerer hvor mye strøm som kan passere gjennom til enhver tid.
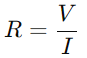 , hvor V er spenning og jeg er aktuell.I hovedsak fungerer motstanden som en flaskehals, og kontrollerer hvor mye strøm som kan passere gjennom til enhver tid.
, hvor V er spenning og jeg er aktuell.I hovedsak fungerer motstanden som en flaskehals, og kontrollerer hvor mye strøm som kan passere gjennom til enhver tid.Kondensatorens funksjon er litt mer intrikat ettersom den midlertidig lagrer elektrisk energi og deretter slipper den tilbake i kretsen.Spenningen over kondensatoren (Vc) korrelerer med den lagrede ladningen (Q) og beregnes ved hjelp av formelen 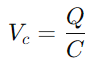 .Dette forholdet fremhever kondensatorens kapasitet til å holde ladning, og påvirker spenningen den utviser direkte.Under drift er dynamikken i lading og utskrivning av kondensatoren avgjørende for å forstå RC -kretsløp.Tidskonstanten (τ), definert som
.Dette forholdet fremhever kondensatorens kapasitet til å holde ladning, og påvirker spenningen den utviser direkte.Under drift er dynamikken i lading og utskrivning av kondensatoren avgjørende for å forstå RC -kretsløp.Tidskonstanten (τ), definert som 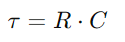 , måler hvor raskt kondensatoren når omtrent 63,2% av full spenning som er levert av kilden (V0).Denne tidskonstanten er en indikasjon på hvordan kretsen tilpasser seg inngangsendringer, med motstands- og kondensatoregenskapene som dikterer tempoet i disse justeringene.
, måler hvor raskt kondensatoren når omtrent 63,2% av full spenning som er levert av kilden (V0).Denne tidskonstanten er en indikasjon på hvordan kretsen tilpasser seg inngangsendringer, med motstands- og kondensatoregenskapene som dikterer tempoet i disse justeringene.
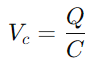 .Dette forholdet fremhever kondensatorens kapasitet til å holde ladning, og påvirker spenningen den utviser direkte.Under drift er dynamikken i lading og utskrivning av kondensatoren avgjørende for å forstå RC -kretsløp.Tidskonstanten (τ), definert som
.Dette forholdet fremhever kondensatorens kapasitet til å holde ladning, og påvirker spenningen den utviser direkte.Under drift er dynamikken i lading og utskrivning av kondensatoren avgjørende for å forstå RC -kretsløp.Tidskonstanten (τ), definert som 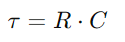 , måler hvor raskt kondensatoren når omtrent 63,2% av full spenning som er levert av kilden (V0).Denne tidskonstanten er en indikasjon på hvordan kretsen tilpasser seg inngangsendringer, med motstands- og kondensatoregenskapene som dikterer tempoet i disse justeringene.
, måler hvor raskt kondensatoren når omtrent 63,2% av full spenning som er levert av kilden (V0).Denne tidskonstanten er en indikasjon på hvordan kretsen tilpasser seg inngangsendringer, med motstands- og kondensatoregenskapene som dikterer tempoet i disse justeringene.Spenningen over kondensatoren når som helst under ladningen er gitt av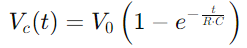 , illustrerer en ikke-lineær økning når kondensatoren fylles.Denne ligningen beskriver hvordan ladningshastigheten bremser når kondensatoren nærmer seg full kapasitet.
, illustrerer en ikke-lineær økning når kondensatoren fylles.Denne ligningen beskriver hvordan ladningshastigheten bremser når kondensatoren nærmer seg full kapasitet.
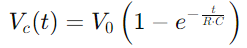 , illustrerer en ikke-lineær økning når kondensatoren fylles.Denne ligningen beskriver hvordan ladningshastigheten bremser når kondensatoren nærmer seg full kapasitet.
, illustrerer en ikke-lineær økning når kondensatoren fylles.Denne ligningen beskriver hvordan ladningshastigheten bremser når kondensatoren nærmer seg full kapasitet.Motsatt, under utslipp, avtar kondensatorens spenning i henhold til 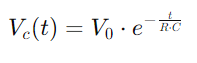 , skildrer en lineær reduksjon i lagret energi over tid.Denne prosessen gir et klart bilde av hvordan energi frigjøres fra kondensatoren tilbake til kretsen.I AC -applikasjoner, faseforskjellen mellom spenning og strøm, φ, blir kritisk.Denne forskjellen, beregnet som
, skildrer en lineær reduksjon i lagret energi over tid.Denne prosessen gir et klart bilde av hvordan energi frigjøres fra kondensatoren tilbake til kretsen.I AC -applikasjoner, faseforskjellen mellom spenning og strøm, φ, blir kritisk.Denne forskjellen, beregnet som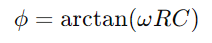 hvor ω Representerer vinkelfrekvens, viser forsinkelsen forårsaket av kondensatoren, noe som påvirker tidspunktet mellom når strømstrømmer og spenning endres over komponentene.
hvor ω Representerer vinkelfrekvens, viser forsinkelsen forårsaket av kondensatoren, noe som påvirker tidspunktet mellom når strømstrømmer og spenning endres over komponentene.
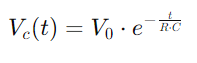 , skildrer en lineær reduksjon i lagret energi over tid.Denne prosessen gir et klart bilde av hvordan energi frigjøres fra kondensatoren tilbake til kretsen.I AC -applikasjoner, faseforskjellen mellom spenning og strøm, φ, blir kritisk.Denne forskjellen, beregnet som
, skildrer en lineær reduksjon i lagret energi over tid.Denne prosessen gir et klart bilde av hvordan energi frigjøres fra kondensatoren tilbake til kretsen.I AC -applikasjoner, faseforskjellen mellom spenning og strøm, φ, blir kritisk.Denne forskjellen, beregnet som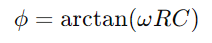 hvor ω Representerer vinkelfrekvens, viser forsinkelsen forårsaket av kondensatoren, noe som påvirker tidspunktet mellom når strømstrømmer og spenning endres over komponentene.
hvor ω Representerer vinkelfrekvens, viser forsinkelsen forårsaket av kondensatoren, noe som påvirker tidspunktet mellom når strømstrømmer og spenning endres over komponentene.Totalt sett begrenser motstanden og styrer strømmen av strøm mens kondensatoren lagrer og modulerer spenningen.Sammen bestemmer de kretsens responsegenskaper, for eksempel hvor raskt den kan lades og utlades og faseforskyvningene som oppstår i vekselstrømsscenarier.Denne kombinerte atferden understøtter de grunnleggende operasjonene av RC -seriekretser, noe som gjør dem integrerte i forskjellige elektroniske applikasjoner.
Grunnleggende ligninger av RC Series Circuit
For å forstå oppførselen til en RC -seriekrets, er det avgjørende å starte med de grunnleggende ligningene som beskriver responsen på endringer i inngangsspenningen.Anta at vi har en skiftende inngangsspenning representert som Vin (T), med spenningen over motstanden merket som VR (T) og over kondensatoren som VC (T).I en seriekrets, den samme strømmen, Den) strømmer gjennom både motstanden og kondensatoren.
Påføring av Kirchhoffs spenningslov (KVL), som sier at den totale spenningen rundt en hvilken som helst lukket sløyfe i en krets må være lik null, finner vi at inngangsspenningen er lik summen av spenningen over motstanden og kondensatoren:

Spenningen over motstanden kan beregnes ved hjelp av Ohms lov:
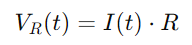
For kondensatoren er spenningen VC (t) relatert til ladningen q (t) den holder, gitt av:
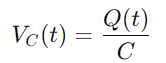
Siden strømmen er definert som ladningsstrømmen, har vi:
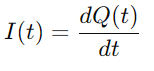
Ved å erstatte Q (t) i ligningen for VC (T), og bruke avledet av ladning Den), Vi utleder kjernedifferensialligningen for RC -seriekretsen:

Ytterligere erstatning Q (t) med integralen av Den), vi får:
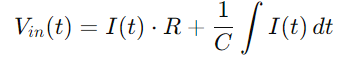
For strømmen I (t), med tanke på endringshastigheten på spenningen over kondensatoren, bruker vi:
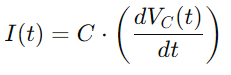
Integrering av alle disse forholdene gir oss differensialligningen som beskriver spenningen over kondensatoren:
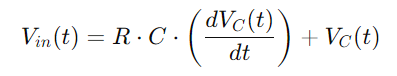
Dette er en førsteordens lineær differensialligning som fanger den tidsavhengige endringen av spenning over kondensatoren.Å løse denne ligningen lar oss nøyaktig beskrive hvordan kondensatorspenningen utvikler seg.Denne forståelsen er grunnleggende for å analysere både lading og utladende sykluser på kondensatoren, så vel som kretsens svar på forskjellige frekvenser.Denne omfattende tilnærmingen gir en dyp innsikt i de dynamiske egenskapene til RC -serien.

Figur 6: Spenningsdifferensialligning
Impedans av RC Series Circuit
For å omskrive beskrivelsen av en RC-seriekrets, med fokus på menneskelig interaksjon og en direkte, forenklet forklaring, la oss forbedre de konkrete opplevelsene og trinn-for-trinn-operasjoner involvert mens vi opprettholder kjernemeldingen og sammenheng:
I en RC -seriekretsarbeid, motstanden og kondensatoren i tandem for å kontrollere strømmen av elektrisitet, avgjørende når du arbeider med vekslende strømmer.Kretsens totale impedans, representert som 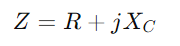 , kombinerer motstanden R og den kapasitive reaktansen XC.Nøkkelfunksjonen i dette oppsettet er at impedansverdiene for begge komponentene varierer med frekvensendringer.Når frekvensen øker, synker impedansen til kondensatoren, slik at mer strøm kan passere gjennom, mens motstanden i det vesentlige forblir konstant.
, kombinerer motstanden R og den kapasitive reaktansen XC.Nøkkelfunksjonen i dette oppsettet er at impedansverdiene for begge komponentene varierer med frekvensendringer.Når frekvensen øker, synker impedansen til kondensatoren, slik at mer strøm kan passere gjennom, mens motstanden i det vesentlige forblir konstant.
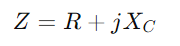 , kombinerer motstanden R og den kapasitive reaktansen XC.Nøkkelfunksjonen i dette oppsettet er at impedansverdiene for begge komponentene varierer med frekvensendringer.Når frekvensen øker, synker impedansen til kondensatoren, slik at mer strøm kan passere gjennom, mens motstanden i det vesentlige forblir konstant.
, kombinerer motstanden R og den kapasitive reaktansen XC.Nøkkelfunksjonen i dette oppsettet er at impedansverdiene for begge komponentene varierer med frekvensendringer.Når frekvensen øker, synker impedansen til kondensatoren, slik at mer strøm kan passere gjennom, mens motstanden i det vesentlige forblir konstant.Impedansen, betegnet som Z og målt i ohm (ω), spiller en kritisk rolle i å bestemme hvordan kretsen reagerer på vekselstrøm.Som i RL -seriekretser, motstanden R og kapasitiv reaktans xC av en RC -krets danner en trekant kjent som impedans -trekanten.Denne trekanten gjelder tett på spenningstrekanten, og ved å bruke Pythagorean teorem, kan du beregne kretsens totale impedans.

Figur 7: RC Series Circuit Beregningsformel
Når det gjelder praktiske applikasjoner, bør du vurdere hodetelefoner, som bruker disse prinsippene.Høydelefoner med høy impedans, ofte over 200 ohm, brukes vanligvis med stasjonære datamaskiner, strømforsterkere og profesjonelt lydutstyr.Disse høyimpedansmodellene stemmer godt overens med utgangsevnen til profesjonell kvalitet.Når du bruker disse hodetelefonene, er det avgjørende å justere volumet gradvis for å unngå overbelastning og skade de delikate interne komponentene, for eksempel stemmespolen.
Motsatt er hodetelefoner med lav impedans, vanligvis under 50 ohm, foretrukket for bærbare enheter som CD-spillere, MD-spillere eller MP3-spillere.Disse hodetelefonene krever mindre strøm for å levere lyd av høy kvalitet, noe som gjør dem ideelle for mobil bruk.Imidlertid krever de også nøye oppmerksomhet på følsomhetsnivåer for å sikre optimal ytelse og forhindre skade på hodetelefonene eller hørselen.

Figur 8: Impedansdiagram over RC -seriekretsen
Inngangs- og analyseprosedyrer for RC -seriekretser
Opptakstiltak Hvor lett en RC -serie krets kan utføre strøm, beregnet som inverse av impedans (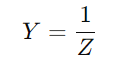 ).Denne verdien integrerer både motstanden (R) og reaktansen (X) av kretsen.Motstand motsetter seg strømstrøm ved å konvertere elektrisk energi til varme, mens reaktans lagrer energi midlertidig i kretsen.
).Denne verdien integrerer både motstanden (R) og reaktansen (X) av kretsen.Motstand motsetter seg strømstrøm ved å konvertere elektrisk energi til varme, mens reaktans lagrer energi midlertidig i kretsen.
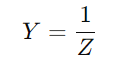 ).Denne verdien integrerer både motstanden (R) og reaktansen (X) av kretsen.Motstand motsetter seg strømstrøm ved å konvertere elektrisk energi til varme, mens reaktans lagrer energi midlertidig i kretsen.
).Denne verdien integrerer både motstanden (R) og reaktansen (X) av kretsen.Motstand motsetter seg strømstrøm ved å konvertere elektrisk energi til varme, mens reaktans lagrer energi midlertidig i kretsen.For å beregne opptak
Begynn med å skrive impedansen 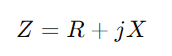 , hvor R står for motstand, X for reaktans, og j er den imaginære enheten.Bruk formelen y = 1/(R + jx).Denne operasjonen involverer komplekse tall og gir oss
, hvor R står for motstand, X for reaktans, og j er den imaginære enheten.Bruk formelen y = 1/(R + jx).Denne operasjonen involverer komplekse tall og gir oss 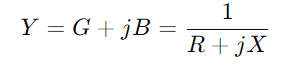 .Her, G er konduktansen (faktisk gjeldende strømningsevne) og B er mottakeligheten (kretsens evne til å reagere på endringer i strøm).
.Her, G er konduktansen (faktisk gjeldende strømningsevne) og B er mottakeligheten (kretsens evne til å reagere på endringer i strøm).
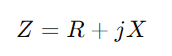 , hvor R står for motstand, X for reaktans, og j er den imaginære enheten.Bruk formelen y = 1/(R + jx).Denne operasjonen involverer komplekse tall og gir oss
, hvor R står for motstand, X for reaktans, og j er den imaginære enheten.Bruk formelen y = 1/(R + jx).Denne operasjonen involverer komplekse tall og gir oss 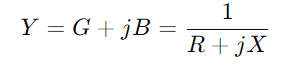 .Her, G er konduktansen (faktisk gjeldende strømningsevne) og B er mottakeligheten (kretsens evne til å reagere på endringer i strøm).
.Her, G er konduktansen (faktisk gjeldende strømningsevne) og B er mottakeligheten (kretsens evne til å reagere på endringer i strøm).
Figur 9: Series RC Circuit Impedance Calculator
Denne beregningen avslører ikke bare kretsens ledningsevne, men også dens dynamiske responsegenskaper, avgjørende for AC -kretsanalyse.Conductance and Semisceptance, samlet, indikerer hvordan kretsen passerer strøm og hvordan den lagrer og frigjør energi.

Figur 10: Fasevinkelformel
Praktisk anvendelse
Ingeniører bruker opptaksverdier for å forbedre kretsdesign, spesielt i høyfrekvente applikasjoner som radiofrekvenskretser.Justering av opptak hjelper til med å samsvare med impedans, redusere signalrefleksjon og øke overføringseffektiviteten.
Ved å studere inngangsresponsen kan ingeniører vurdere og forutsi kretsytelse under forskjellige forhold som frekvensrespons, stabilitet og følsomhet.Utstyr med et oscilloskop og en signalgenerator for å måle kretsens spenning og strøm ved varierende frekvenser.Fokuser spesielt på avskjæringsfrekvensen for å teste teoretiske spådommer og validere dem mot praktiske observasjoner.For vekselstrømskretser, begynn med å bestemme reaktansen (XC) til kondensatoren med 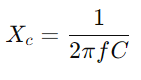 , hvor f er signalfrekvensen.Beregn den totale impedansen
, hvor f er signalfrekvensen.Beregn den totale impedansen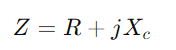 og deretter opptak
og deretter opptak 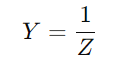 .
.
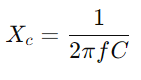 , hvor f er signalfrekvensen.Beregn den totale impedansen
, hvor f er signalfrekvensen.Beregn den totale impedansen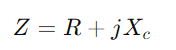 og deretter opptak
og deretter opptak 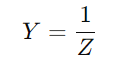 .
.Analysere faseforskjell ved bruk av 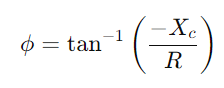 For å forstå signalformendring.Undersøk hvordan kretsen håndterer forskjellige frekvenser, spesielt å merke oppførselen ved avskjæringsfrekvensen
For å forstå signalformendring.Undersøk hvordan kretsen håndterer forskjellige frekvenser, spesielt å merke oppførselen ved avskjæringsfrekvensen 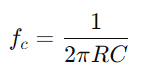 , der kretsen skifter fra passering til blokkering av signaler.Å evaluere hvordan impedans og faseforskjell varierer med frekvens, er avgjørende for å designe effektive filtre og signalprosessorer.Diskuter hvordan frekvensselektivitet, faseskift og signaldemping på grunn av kretsens egenskaper påvirker praktiske anvendelser som filtrering og elektronisk innstilling.
, der kretsen skifter fra passering til blokkering av signaler.Å evaluere hvordan impedans og faseforskjell varierer med frekvens, er avgjørende for å designe effektive filtre og signalprosessorer.Diskuter hvordan frekvensselektivitet, faseskift og signaldemping på grunn av kretsens egenskaper påvirker praktiske anvendelser som filtrering og elektronisk innstilling.
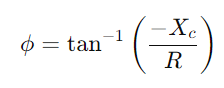 For å forstå signalformendring.Undersøk hvordan kretsen håndterer forskjellige frekvenser, spesielt å merke oppførselen ved avskjæringsfrekvensen
For å forstå signalformendring.Undersøk hvordan kretsen håndterer forskjellige frekvenser, spesielt å merke oppførselen ved avskjæringsfrekvensen 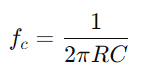 , der kretsen skifter fra passering til blokkering av signaler.Å evaluere hvordan impedans og faseforskjell varierer med frekvens, er avgjørende for å designe effektive filtre og signalprosessorer.Diskuter hvordan frekvensselektivitet, faseskift og signaldemping på grunn av kretsens egenskaper påvirker praktiske anvendelser som filtrering og elektronisk innstilling.
, der kretsen skifter fra passering til blokkering av signaler.Å evaluere hvordan impedans og faseforskjell varierer med frekvens, er avgjørende for å designe effektive filtre og signalprosessorer.Diskuter hvordan frekvensselektivitet, faseskift og signaldemping på grunn av kretsens egenskaper påvirker praktiske anvendelser som filtrering og elektronisk innstilling.Denne tilnærmingen bryter ned de operasjonelle prosessene til håndterbare trinn, og beriker brukerens forståelse med praktisk innsikt i håndtering og analyse av RC -seriekretser.

Figur 11: Kjennetegn på RC -seriekretser
Phasor Diagram of RC Series Circuit
I en RC -seriekrets deler alle elementer samme strøm på grunn av seriekonfigurasjonen.Denne ensartede strømmen fungerer som en grunnlinje for fasordiagrammet vårt, noe som hjelper til med å visualisere forholdet mellom forskjellige spenninger og strømmer i kretsen.La oss utpeke denne nåværende jeg som referansefasor, plassert i null grader på diagrammet.I diagrammet, strømmen jeg settes horisontalt til høyre, og etablerer nullgrads referanselinjen.Spenningen over motstanden (UR) er i fase med strømmen fordi motstander ikke forårsaker noen faseskift.Slik, UR trekkes som en horisontal vektor i samme retning som jeg, strekker seg fra opprinnelsen.

Figur 12: RC Series Circuit Phasordiagram
I kontrast til spenningen over kondensatoren (UC) Leder strømmen med 90 grader på grunn av den kapasitive egenskapen ved å utsette den nåværende fasen.Denne spenningen er representert av en vertikal vektor som peker oppover, og starter fra spissen av UR vektor.Den totale spenningen U I kretsen er vektorsummen av U Rand UC.Denne summen danner en riktig trekant med UR og UC som henholdsvis de tilstøtende og motsatte sider.Hypotenusen til denne trekanten, som strekker seg fra opprinnelsen til spissen av UC vektor, representerer U.
Sinusformede strøm gjennom kretsen er gitt av synd (ωt), hvor jeg er den maksimale strømamplitude og ω er vinkelfrekvensen.Følgelig er spenningen over motstanden 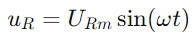 , speiler den nåværende bølgeformen.Spenningen over kondensatoren er gitt av
, speiler den nåværende bølgeformen.Spenningen over kondensatoren er gitt av 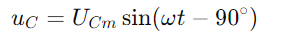 , som indikerer et faseforskyvning på −90 ° (eller 90 grader foran strømmen).Fasordiagrammets høyre trekant tydeliggjør det
, som indikerer et faseforskyvning på −90 ° (eller 90 grader foran strømmen).Fasordiagrammets høyre trekant tydeliggjør det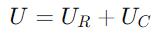 er ikke bare i størrelsesorden, men også i faseforhold, med terminalspenningsvektoren (U) fullføre trekanten.
er ikke bare i størrelsesorden, men også i faseforhold, med terminalspenningsvektoren (U) fullføre trekanten.
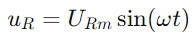 , speiler den nåværende bølgeformen.Spenningen over kondensatoren er gitt av
, speiler den nåværende bølgeformen.Spenningen over kondensatoren er gitt av 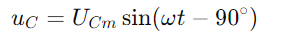 , som indikerer et faseforskyvning på −90 ° (eller 90 grader foran strømmen).Fasordiagrammets høyre trekant tydeliggjør det
, som indikerer et faseforskyvning på −90 ° (eller 90 grader foran strømmen).Fasordiagrammets høyre trekant tydeliggjør det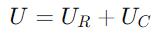 er ikke bare i størrelsesorden, men også i faseforhold, med terminalspenningsvektoren (U) fullføre trekanten.
er ikke bare i størrelsesorden, men også i faseforhold, med terminalspenningsvektoren (U) fullføre trekanten.
Figur 13: Spenningsfasordiagram over RC -seriekretsen
Nøkkelpunkter i analysering av serie RC -kretser
Impedans i serie RC -krets, representert som Z, kombinerer motstand (R) og den reaktive effekten av kapasitans til et enkelt tiltak som varierer med signalfrekvens.Det uttrykkes matematisk som 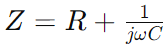 , hvor ω er vinkelfrekvens og C er kapasitansen.Her, R utgjør den virkelige delen av impedansen, og
, hvor ω er vinkelfrekvens og C er kapasitansen.Her, R utgjør den virkelige delen av impedansen, og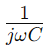 representerer den imaginære delen, som indikerer hvordan kondensatoren påvirker kretsen.
representerer den imaginære delen, som indikerer hvordan kondensatoren påvirker kretsen.
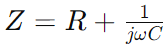 , hvor ω er vinkelfrekvens og C er kapasitansen.Her, R utgjør den virkelige delen av impedansen, og
, hvor ω er vinkelfrekvens og C er kapasitansen.Her, R utgjør den virkelige delen av impedansen, og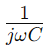 representerer den imaginære delen, som indikerer hvordan kondensatoren påvirker kretsen.
representerer den imaginære delen, som indikerer hvordan kondensatoren påvirker kretsen.Måten impedans endres med frekvens er sentralt for bruk av RC -kretser i filtrering av applikasjoner.Ved lavere frekvenser viser kretsen høyere impedans, og blokkerer effektivt disse frekvensene.Motsatt, ved høyere frekvenser, synker impedansen, slik at disse frekvensene kan passere mer fritt.Denne oppførselen gjør serie RC-kretser ideelle for oppgaver som å filtrere ut uønsket lavfrekvensstøy eller passere høyfrekvente signaler.

Figur 14: Impedansvektordiagram over RC -seriekretsen
Konklusjon
Fra filtrering av uønskede frekvenser til forming av signalresponser, er RC -seriekretsen instrumental i et bredt spekter av elektroniske funksjoner.Ved å forstå de underliggende prinsippene som impedans, fasorforhold og den frekvensavhengige oppførselen til disse kretsløpene, er ingeniører og designere utstyrt til håndverksløsninger som effektivt administrerer signalintegritet i komplekse elektroniske systemer.Den detaljerte undersøkelsen av disse kretsløpene, støttet av matematisk analyse og visuelle representasjoner som fasordiagrammer, tilbyr en omfattende innsikt som er viktig for alle som ønsker å utdype forståelsen av elektronisk kretsdynamikk eller for å forbedre deres praktiske ferdigheter i kretsdesign og feilsøking.
Ofte stilte spørsmål [FAQ]
1. Hva er prinsippet om RC Circuit?
Prinsippet om en RC-krets (motstandskapacitor) dreier seg om lade- og utladingsprosessene til kondensatoren gjennom motstanden.I denne kretsen samhandler kondensatorens evne til å lagre og frigjøre elektrisk energi med motstanden, som kontrollerer hastigheten som kondensatoren lades eller slipper ut.
2. Hvorfor fører en RC -krets strøm?
I en RC -krets fører strømmen spenningen over kondensatoren fordi kondensatoren må begynne å lade før spenningen kan stige.Siden strømmen strømmer inn i kondensatoren for å lade den, topper strømmen før spenningen over kondensatoren når sitt maksimum.Denne effekten forårsaker et faseskifte der strømfasen fører spenningsfasen med opptil 90 grader, avhengig av frekvensen av inngangssignalet.
3. Hvordan endres spenningen i en RC -krets?
Spenningsendringen i en RC -krets under lading er beskrevet av en eksponentiell funksjon.Når en spenning påføres, øker spenningen over kondensatoren i utgangspunktet raskt, og bremser deretter når den nærmer seg forsyningsspenningen.Matematisk er dette uttrykt som 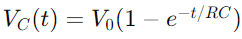 , hvor VC(t) er spenningen over kondensatoren på tidspunktet T, V0 er forsyningsspenningen, og RC er tidskonstanten for kretsen, og bestemmer hvor raskt kondensatoren lades.Motsatt, under utlading, reduserer spenningen over kondensatoren eksponentielt, etter ligningen
, hvor VC(t) er spenningen over kondensatoren på tidspunktet T, V0 er forsyningsspenningen, og RC er tidskonstanten for kretsen, og bestemmer hvor raskt kondensatoren lades.Motsatt, under utlading, reduserer spenningen over kondensatoren eksponentielt, etter ligningen 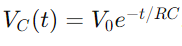 .
.
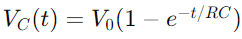 , hvor VC(t) er spenningen over kondensatoren på tidspunktet T, V0 er forsyningsspenningen, og RC er tidskonstanten for kretsen, og bestemmer hvor raskt kondensatoren lades.Motsatt, under utlading, reduserer spenningen over kondensatoren eksponentielt, etter ligningen
, hvor VC(t) er spenningen over kondensatoren på tidspunktet T, V0 er forsyningsspenningen, og RC er tidskonstanten for kretsen, og bestemmer hvor raskt kondensatoren lades.Motsatt, under utlading, reduserer spenningen over kondensatoren eksponentielt, etter ligningen 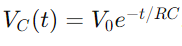 .
. OM OSS
Kundetilfredshet hver gang.Gjensidig tillit og felles interesser.
OM OSS
Kundetilfredshet hver gang.Gjensidig tillit og felles interesser.
funksjonstest.De høyeste kostnadseffektive produktene og den beste tjenesten er vårt evige engasjement.
Hot artikkel
- Er CR2032 og CR2016 utskiftbare
- MOSFET: Definisjon, arbeidsprinsipp og utvalg
- Reléinstallasjon og testing, tolkning av relé koblingsdiagrammer
- CR2016 vs. CR2032 Hva er forskjellen
- NPN vs. PNP: Hva er forskjellen?
- ESP32 vs STM32: Hvilken mikrokontroller er bedre for deg?
- LM358 Dual Operational Amplifier Omfattende guide: Pinouts, kretsdiagrammer, ekvivalenter, nyttige eksempler
- CR2032 vs DL2032 vs CR2025 sammenligningsveiledning
- Forstå forskjellene ESP32 og ESP32-S3 teknisk og ytelsesanalyse
- Detaljert analyse av RC Series Circuit
 Dybdeanalyse av 1N4148 Dioder: Driftsmodus, spesifikasjoner og bruksscenarier
Dybdeanalyse av 1N4148 Dioder: Driftsmodus, spesifikasjoner og bruksscenarier
2024-05-08
 Forstå typene og bruken av dynamiske og positive forskyvningspumper
Forstå typene og bruken av dynamiske og positive forskyvningspumper
2024-05-07
Hot delnummer
 C1608CH2A681J080AA
C1608CH2A681J080AA C0603C0G1E2R8C030BG
C0603C0G1E2R8C030BG 0603YC392MAT2A
0603YC392MAT2A CC1206JRNPOBBN390
CC1206JRNPOBBN390 06031C472JAZ2A
06031C472JAZ2A 04023A271KAT2A
04023A271KAT2A 06035A360FAT2A
06035A360FAT2A TPSB107K004R0350
TPSB107K004R0350 EPM7160EQC160-20
EPM7160EQC160-20 DS21348TN
DS21348TN
- EPM7256AETI144-7
- PIC24FJ256GA106-I/MR
- MAX4533CAP+
- CY7C09449PVA-AC
- SP000063852
- 78B08ST
- 7MBR10SA120-70
- BSM1200GA120DN2
- CM30AD12A-12H
- MCC95-04io1B
- LTC3770EUH#TRPBF
- DS90CR281MTD
- S912ZVML32F3VKH
- XC18V02PC44I
- MBRB40250TG
- CD4052BNSR
- LT1129IS8-5#TRPBF
- T491B475M010AT4380
- TPA4861D
- TPSB336K010T0250
- T491A106M010ZTZ001
- CMSH2-100MTR13
- ICS476G10LF
- LP3995ITL-2.8
- MAX1162BCUB
- MC145480DW
- S19219PBI20
- SI4532ADY
- SPL08A2-16C
- TC74HC132AF
- TDA7498MV
- LH16374EP
- M44C260I
- QL4009-OPL84C
- TXS0104EZXU
- R5F2LA66ADFP
- 88E1119RXX-NNW2I000
- FS32K116LFT0MLFR
- G6B-2214P-USDC5